LevelDB学习：前置知识

前言：

在完成Epidemic第一阶段后，我发现在数据存储部分的设计没有学习到更多知识，因此通过对LevelDB的学习了解一下在实际项目中对于数据的存储是如何设计与实现的。

由于LevelDB是我接触的新领域，因此在学习LevelDB之前需要补充一下前置知识，这样方便后续对LevelDB结构设计与源码阅读的理解。

Varint

Varint 是一种紧凑的表示数字的方法。它用一个或多个字节来表示一个数字，值越小的数字使用越少的字节数。这能减少用来表示数字的字节数。
在编程中表示整数的类型通常是int32,int64。但是我们在使用的时候并不会完全利用所有的位数，比如1，2，300等数字，这样的话会浪费大量的位数，因此对于很小的int32位数字，可以用1个byte来表示。但这样的缺点就是大数字需要5个byte表示。不过在系统中小数字还是占大多数的，因此采用Varint从整理来看能节省更多的存储开销。

Varint格式

Varint中的每个byte的最高位bit有特殊的含义：

1：后续的byte也是该数字的一部分
0：统计结束

因此1个byte中用于存储数字的位数为7位，在Varint中1个byte最高能表示的数字大小为：127，超过这个值就需要用2个byte表示。
注意的一点是Varint采用小端字节序，对于二进制来说左边才是低位。

Varint编解码

取一个数字300，用二进制表示为：0000 0001 0010 1100。将其用Varint编码后得：1010 1100 0000 0010。由于每个byte的首位都有特殊含义，在第一个byte中首字节是1，表示后续的byte也是该数字的一部分，因此得到的结果为：_010 1100 _000 0010。由于是小端字节序，所以在重新排序后得到结果为：_000 0010 _010 1100，去掉Varint的特殊位后得到：0001 0010 1100。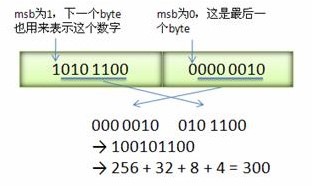

对于有符号的数字

从上可知Varint并不能表示负数，因此Google采用zigzag编码来替代。zigzag采用正数和负数交错的方式来同时表示无符号数来表示有符号数字，如图所示：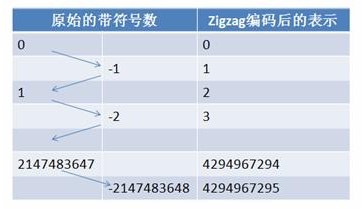

使用zigzag编码，绝对值小的数字，无论正负都可以采用较少的byte来表示，充分利用了Varint这种技术。

Varint实现

private static int encoder(int num) {
    int result = 0;
    while (num > 0) {
        byte n = (byte) (num & 0b1111111);
        num >>= 7;
        result <<= 8;
        if (num > 0) {
            result += n ^ 0b10000000;
        } else {
            result += n;
        }
    }
    return result;
}

private static int decoder(int num) {
    int result = 0;
    while (num > 0) {
        result <<= 7;
        byte n = (byte) (num & 0b11111111);
        // int tag = (n & 0b10000000) >> 7;
        //System.out.println("tag:" + tag);
        byte m = (byte) (n & 0b1111111);
        result ^= m;
        num >>= 8;
    }
    return result;
}

CRC

CRC校验用于检验文件与请求的完整性。并且在校验值不匹配的情况下，可以针对数据损坏采取纠正措施。
之所以称为 CRC，是因为校验（数据验证）值是一种冗余（它在不添加信息的情况下扩展消息）并且该算法基于循环码。CRC 很受欢迎，因为它们易于在二进制硬件中实现，易于数学分析，并且特别擅长检测由传输通道中的噪声引起的常见错误。由于校验值具有固定长度，生成它的函数偶尔会用作散列函数。
CRC基于循环纠错码的理论，通过添加固定长度的校验值对消息进行编码，用于通信网络中的错误检测。CRC 码的规范需要定义一个所谓的生成多项式，该多项式成为多项式长除法中的除数，将消息作为被除数，其中商被丢弃，余数成为结果。
通常是n-bit CRC 应用于任意长度的数据块将检测任何不超过n位的单个错误突发，并且它将检测到的所有较长错误突发的分数是(1 − 2−n )。当校验值为n位长时，CRC 称为n位 CRC 。

缺点

CRC专门用于信道通信上的非人为影响的问题，如果是人为故意的，攻击者可以在修改数据后重新编码CRC，在这种没有身份验证的情况下是无法区分的。
CRC编码是可逆的，这使得它不适合应用在数字签名中。
CRC是一个线性函数，具有有限等效保密协议的设计缺陷，容易被反向恢复密钥导致关键信息泄漏。

计算

要计算n位的CRC，首先需要将表示输入的位排成一行，并将表示CRC除数（即多项式）的n+1位模式放置在行的左下方。

例子

设：

CRC的位数为3
多项式为：x³+x+1
消息的位数为14

首先将多项式用二进制写成系数，得：1 x^{3</^{> + 0}} x² + 1 * x + 1，在这种情况下，系数为1、0、1和1。计算的结果是3位长，因此这是一个3-CRC。但是我们需要4位来说明多项式。
等待编码的消息为：11010011101100
首先，用CRC对应位数个数的0填充。这样做是为了使字节码具有系统形式。这是计算3位CRC的第一步计算：

11010011101100 000    <---- 输入右填充3位
1011    <---- 除数（4位） = x3+x+1
-----------------------------------------
01100011101100 000    <---- 结果
该算法作用于每一步中除数上方的位，迭代的结果是多项式与上方位的按位异或（相同为0，不同为1）。这一步完成后将结果重新进行计算，但是在开始的时候将除数右移直到与新的输入左边的1对应：
11010011101100 000 <--- 输入右填充 3 位
1011 <--- 除数
01100011101100 000 <--- 结果（注意前四位是与下面除数的异或，其余位不变）
 1011 <--- 除数...
00111011101100 000
  1011
00010111101100 000
   1011
00000001101100 000 <--- 请注意，除数移动以与被除数中的下一个 1 对齐（因为该步骤的商为零）
       1011（换句话说，它不一定每次迭代移动一位）
00000000110100 000
        1011
00000000011000 000
         1011
00000000001110 000
          1011
00000000000101 000
           101 1
-----------------
00000000000000 100 <--- 余数（3 位）。

除法算法在此处停止，因为正体的消息中已经全部为0.
由于除数每次都移动到结果最左端1的位置，最终的结果是待编码的位数都为0，最终结果中唯一可以为非0的区域是输入右边填充的n位，而这n位就是CRC的结果。

代码

/**
* @param value 待编码的树
* @param fnc 除数
*/
public static int check(int value, int fnc) {
    //后期待编码的数字的长度
    int valueLen = readIntLen(value);
    //CRC的位数
    int fncLen = readIntLen(fnc) - 1;
    // 往右填充后的值
    int n = value << fncLen;
    for (int i = 0; i < valueLen; i++) {
        int nLen = readIntLen(n);
        if (nLen <= fncLen) {
            break;
        }
        //除数要移动的位数
        int moveLen = nLen - fncLen - 1;
        int nFnc = (fnc << moveLen);
        n = n ^ nFnc;
    }
    return n;
}

/**
* 获取n的长度，
* @param n 计算到从最高位的1为止
*/
private static int readIntLen(int n) {
    int result = 0;
    while (n > 0) {
        n >>= 1;
        result += 1;
    }
    return result;
}

Snappy压缩

Snappy是一个压缩/解压库。它的目标不是最大压缩，也不是与其他任何压缩库兼容。它的目标是为了实现最快压缩与合理压缩。
Snappy具有以下属性:

快速：压缩速度为 250 MB/秒及以上，无需汇编代码。
稳定：在过去几年，Snappy 在 Google 的生产环境中压缩和解压了数 PB 的数据。Snappy 比特流格式是稳定的，不会在版本之间发生变化。
健壮：Snappy 解压器的设计不会在遇到损坏或恶意输入时崩溃。

可以说，Snappy最大的优点就在于快速压缩。

LevelDB中的使用

在LevelDB中，默认就开启了Snappy压缩，用于对写入的数据进行快速压缩，这可以在保证写入速率的情况下节省空间。
对于LevelDB来说，这些优化方案不能够牺牲读写速度，因此采用Snappy，在保证速度的同时还能够获取一定的磁盘空间。

互斥锁

互斥锁是悲观锁的一种，当线程在获取竞争资源时无论是读还是写，都需要先获取到该资源的锁。它能保证在同一时刻竞争资源只会被一个线程修改。

跳表(Skip list)

跳表是使用概率平衡而不是严格强制平衡的数据结构。因此，跳表的插入和删除算法比平衡树的等效算法简单得多，速度也快得多。
二叉树在插入随机顺序的元素的时候工作的很好，但是一旦按顺序插入元素，他就会退化为链表导致性能下降。由此产生了平衡树算法，在执行操作的时候重新排列树以保持平衡。
跳表是平衡树的概率替代方案。它通过随机数生成器来平衡树。在理论上跳表也是能够退化为链表（多个随机数生成为顺序的情况），但是这种情况发生的比例很低，且没有任何输入序列能够连续产生最坏情况。（随机主元素的快速排序）
跳表具有类似于随机插入构建的搜索树的平衡性，但实际使用中不需要随机插入。

跳表与平衡树的优势

跳表的实现比平衡树更简单；
通过概率去平衡数据结构比明确地保持平衡更容易；
跳表随着数据的插入操作速度是恒定增加的；
跳表比平衡树节省空间。

实现推理

设：

给定一个长度为n的链表
链表中的元素按顺序存储

在搜索链表时，可能要检查每个节点：
如果链表按顺序排列，给每两个节点一个指向链表中后两个节点的指针，由此在原有的基础上构建出原长度的1/2长的链表，此时我们只需要检查n/2+1个节点：
按照上述步骤继续增加间隔，此时是新增每四个节点建立一个指针，检查链表只需要n/4+2：
如果每个节点前面有一个指针指向2i节点，则必须检查的节点数量可以减少到log₂n：

但是这种数据结构只方便用于快速搜索，无法有效地插入删除。

具有k个前向指针的节点称为k级节点。如果每个第2i个节点前面都有一个指针2i节点，那么节点的级别有简单的模式分布：50%是级别1，25%是级别2，12.5%是级别3，以此类推。如果节点的级别是随机选择的，但是比例相同如下：

此时一个节点的第i个前向指针不是指向前面的2i个节点，而是志向下一个i级或者更高级别的节点。此时插入删除只需要局部修改；节点的级别是在插入节点时随机选择的，永远不需要改变。某些级别的安排会导致执行时间很短，但这种安排会很少见。因为这些数据结构是带有跳过中间节点的额外指针的链表，所以我们将其称为跳表。

在分配节点等级阶段就引入随机，但是在宏观上却保持一个准确值，在这里体现的就是跳表的比例正确，但是跳表节点出现的地点随机，这样在一个小表中可以方便地进行插入删除操作，对整体的读取速度影响较小，因为在宏观上多级节点数量比例是正确的。

算法详情

每个元素由一个节点表示，节点的级别在插入节点时随机选择，而不考虑数据结构中的元素数量。第i级节点有i个前向指针，索引从1到i。在节点中不需要存储节点的级别。级别上限为某个适当的常量MaxLevel。列表的级别是列表中当前的最大级别（如果列表为空，则为1）。
列表的标题在第一级到MaxLevel有前向指针。级别高于列表当前最大级别的标头的前向指针指向NIL

NIL类似于一个null节点，用来标识检索结束

初始化

一个元素NIL被分配并被赋予一个大于任何合法键的键。所有跳过列表的所有级别都以NIL终止。
初始化一个新列表，使列表的级别等于1，并且列表头的所有前向指针都指向NIL。

在初始化阶段创建一个NIL与初始节点

搜索算法

这是搜索的伪代码，这部分图片需要和上面的跳表结构对照着理解。

首先是list的定义，list表示跳表最左边的那一系列head集合，查询时的迭代顺序从上到下，也就是这样：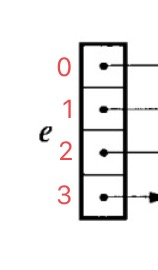

注意，这里我排的顺序是反的，按照伪代码来说正确level顺序应该是从上往下表示为：3、2、1、0。问题不大～

而list -> level就是当前x所在的节点的层数，迭代是从0开始往下，而其中的forward[i]表示的是当前节点所指向的节点。
让我们从上面的跳表中查询21吧，首先x=list->header,他现在位于header的第一位：

它的level为4，但是当i为0，即在最开始的位置的时候，forward[0]->kay = 6，此时6 < 21，所以在这一区间的所有值都小于等于6（表示为(-∞, 6]），因此直接跳到6所在的节点。

然后在6中i还是为0，但这时候forward[0]所指向的值为NIL，表示已经到了末尾（表示为[6, +∞)）。在这一区间是可能存在21的，因此需要让i+1，去查找下一层的节点。

此时forward[1]所指向的值为25，这表示已经寻找到了一个区间[6, 25]，而我们的21是存在这个区间内的，因此继续往下级寻找

此时forward[2]所指向的值为9，在[6, 9]不满足条件，在伪代码中表现为forward[2]->key < searchKey，因此将指针指向9所在的节点。

这样，通过不断细化区间，最终在最后一级的链表中确定一条值包含要查询的key的链表，通过顺序查找来确定这条子链表中是否包含21.

插入与删除算法

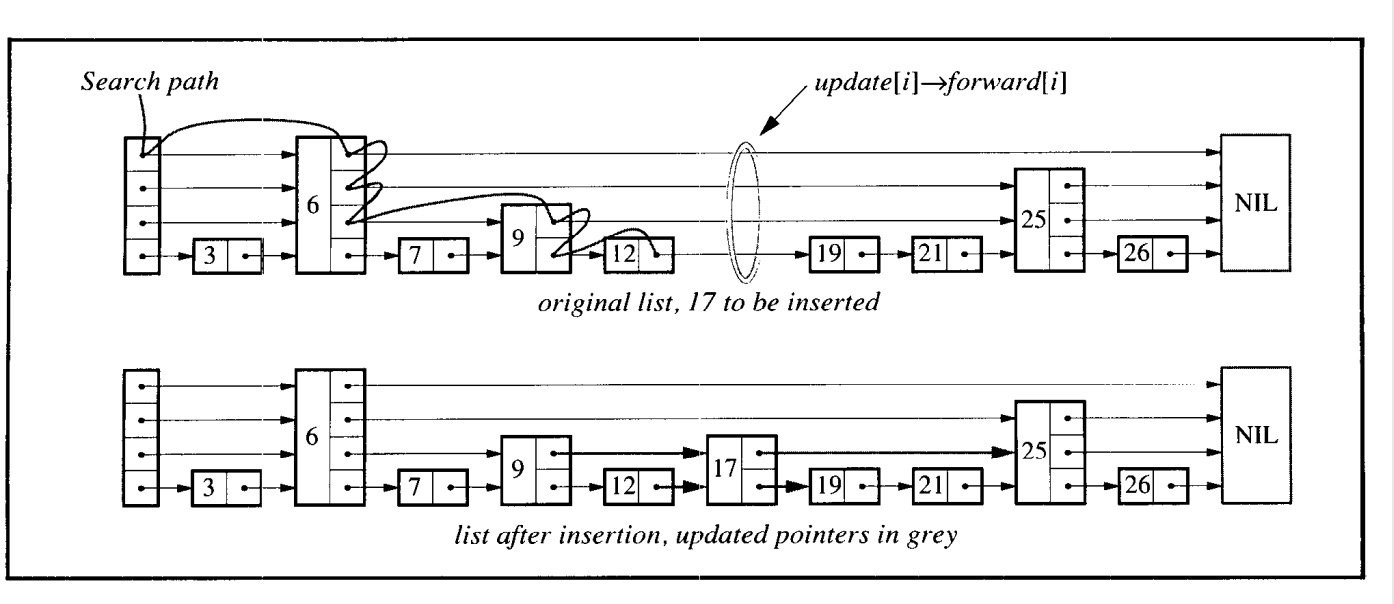
若要插入，则可以直接采用搜索+拼接的方式。

伪代码如下：

维护向量更新，以便当搜索完成（准备执行拼接）时，update[i]包含指向第i级或更高级别的最右侧节点的指针，该节点位于插入位置的左侧。
插入时最重要的一点就是随机生成的level函数。

随机选择Level

Level是在不参考元素数量的情况下随机生成：

这里设置了一个初始值newLevel，并通过随机数生成函数判断生成的随机数是否小于p，如果小于p则newLevel+1，返回newLevel与MaxLevel的最小值。
这里通过随机数概率的形式获取一个随机的Level。

注意这里的p，表示生成的[0, 1)的随机数小于p的时候level+1，在伪代码中作者给的是0.5，在redis中给出的是0.25，但是我在其他地方听人说最佳的比例应该是2.7这个自然对数，用在这里就是0.27？
补充：在查询计算复杂度时，期望复杂度为log_aN,其中a = p^-p，在p=e时取得最小值。

LSM-Tree

见这篇文章：初探LSM-Tree

Env

include/leveldb/env.h中包含了关于文件目录操作及其他相关函数调用的封装，比如文件锁，线程创建及启动等。通过Env类，将系统相关的底层调用和操作进行了封装。这样用户就可以通过实现自己的Env，将LevelDB架在不同的文件系统上。用户只需要实现自己的Env，然后通过Options在OpenDB时传递给它，这样这些相应的操作就会使用用户自己的实现了。

LevelDB提供了针对底层文件系统操作的自定义配置。

快照（Snapshot）

LevelDB支持Snapshot，用户需要首先创建某一个时刻的Snapshot，之后在读取时设置ReadOptions::snapshot就可以读取之前那个时刻的Snapshot，实际上通过Snapshot维护了关于整个key-value存储状态的一致性的只读视图。
Snapshot关联了一个sequence number，每次创建Snapshot之后该编号都递增。当系统要回滚到某个时刻的时候在读取数据时跳过大于该sequence number的所有记录。但是实际大于该sequence number的所有记录并不会被删除，而是会被标记为compact，方便版本回归到最新。
sequence number会被记录在versions_中。每次用户执行一个更新操作时，它都会+1，所以说sequence number在这里体现的不是操作发生的时间，而是对操作的计数，当然sequence number越大也说明操作越新。

问题

在了解了前置知识后我对LevelDB抱有很多疑问，因此后面就带着这些问题去学习LevelDB：

SSTable大小如何划分
rolling merge过程是如何实现的，是跟论文原文一样将C0部分/全部数据跟C1全部数据组合还是如何
磁盘组件索引在内存中是如何展现的，即这部分数据在内存中是以什么形式展示的
rolling merge过程中对并发访问是如何解决的
checkpoint是如何创建以及使用的
查询/添加/删除操作的具体实现步骤
sstable的具体结构实现
memtable到sstable的数据结构转换过程