如何准确地估算LSM-Tree中各个组件地阈值大小是一个数学问题。但是在实际计算过程中为了简化计算,所求出的最终结果会是一个近似值而不是准确的数值。
对于计算机来说差的那点数值在计算时间的表现上并不明显。
题外话:我发现论文中的数学推导很多数据都不知道是从哪里来的。还是要问问相关人士。
前言
首先需要确定影响组件大小的因素以及对他们的假设:
- π:磁盘以multi-page blocks为单位读写一个page时的开销
- p:磁盘随机读写一个page的开销
- M:从C0中merge到C1中的一个page-sized的叶节点中的记录的平均数目
- d:1MB磁盘存储开销
- m:1MB内存存储开销
- H:每秒H个磁盘页面访问的的IO传输需求
- S:数据存储总量
开销的计算
对于磁盘来说,如果磁盘容量是瓶颈,则在磁盘填满时应用程序只使用了磁盘磁臂所提供的IO能力的一部分;反过来,如果我们发现在添加数据时,磁盘磁臂已经被充分使用,但是磁 盘还有剩余空间,这就意味着IO能力是瓶颈。
这个结论很重要,因为对于我们来说,在任何时候这两种开销总会有一种成为访问瓶颈。因此应用程序针对磁盘的访问开销D就是:
D = max(H·p, S·d) -> 访问开销=max(数据存储总开销,数据访问的IO开销)
在没有缓存的情况下D就是应用程序支持数据S访问的总开销T。如果在S不变的情况下,应用程序针对磁盘的总开销随着IO的访问频率H成线性增长。当IO的开销H·p超过磁盘开销S·d后可以引入内存缓存来取代磁盘IO。这个时候就表示数据的访问频率高到IO使用率达到100%但是依旧有大量的请求没有得到IO。那么在这种情况下磁盘的开销就又只取决于所需的磁盘存储空间,此时访问数据的开销B就可以简单地表示为内存的开销与磁盘存储的开销:
B = S·m + S·d -> 相当于将磁盘中的所有数据都载入内存
此时用于支持应用程序的数据访问的总开销T就是由D和B的最小值决定的:
T = min(max(H·p, S·d), S·m + S·d)
由此可以画出数据访问总开销与访问H/S的关系,其中COST-TOT=T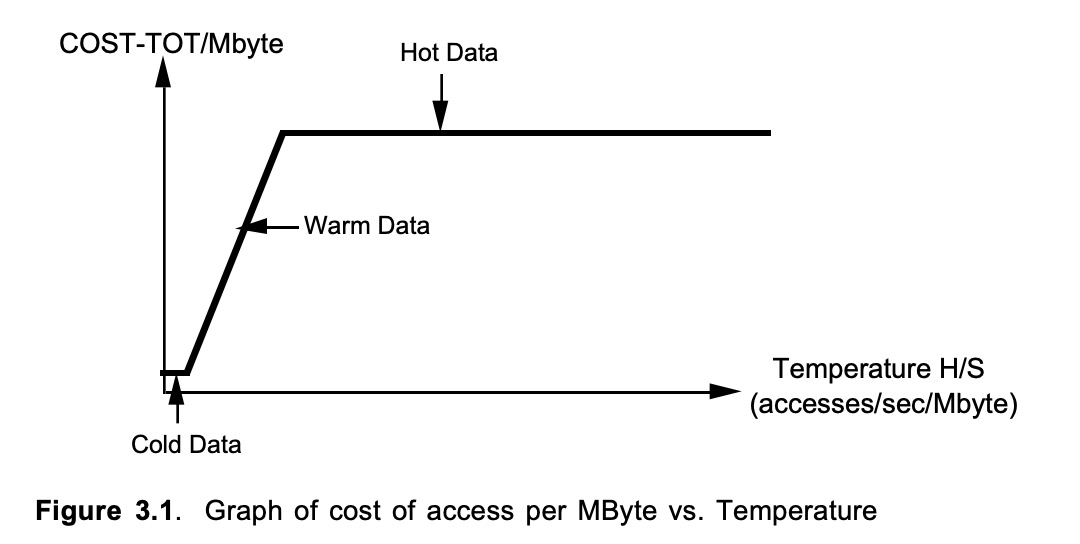
组件大小的计算
设:
- Si:表示组件Ci的大小
- S:表示LSM-Tree所有组件大小之和,S=S0+S1+…Sk
- Sp:页大小(以bytes为单位)
- R:针对C0的插入速率,单位bytes/秒。为了方便计算,这个速率是相对平稳的数值,即一个常量
- H:每秒H个磁盘页面访问的的IO传输需求
- ri:相临两个组件大小只比。ri = Si/Si-1 (i=1,2…k)
- 所有的组件Ci都有一个相对固定的大小(因为删除会和会将插入抵消掉,因此实际的Ci大小是会变化的)
- 不同组件的blocks将会以混合的方式使用不同的磁盘,以达到磁盘磁臂利用率的平衡
这样最小化H就等价于最小化总的磁盘磁臂开销
前提这是是IO开销大于磁盘存储开销的情况
由此我们可以得到一个问题:对于给定的R,找到可以使总的IO请求率H最小化的ri值。
对于S,我们可以得到:
S = S0 + r1·S0 + r1·r2·S0+…
在总S固定不变的前提下,由于ri的变化会使的问题复杂化,但是当假设Sk也是固定不变的时候,由于S与Sk是固定的,则当所有的ri值等于某个常数r时,就可以取得最小值。此时可以用S与S0来表示r:
S = S0 + r.S0 + r2.S0 + . . . + rk.S0
我们假设数据在到达Ck之前都不会被删除,因此对于C0的数据插入速率与Ci-1到Ci的数据移出速率应该是一样的(0 < i ≤ k)。
当Ci-1为磁盘组件的情况,从Ci-1到Ci的rolling merge过程将会包含从Ci-1中以每秒R/Sp个page的multi-page block读取。该合并过程还会包含从Ci中以每秒ri·(R/Sp)个page的multi-page block读取(这是因为在merge过程中在Ci中扫描的page数量是Ci-1的ri倍)。最后,数据还会以每秒(r+1)·(R/Sp)个page的multi-page磁盘写入来将属于Ci的新merge出来的数据写入。(由于merge引起导致Ci组件的增大,因此数据成为了(r+1)·(R/Sp)个page)。将所有的组件的Ci对应值相加,就可以得到总的multi-page IO大小H(以每秒的page数为单位):
H=(R/Sp)·((2·r1+2) + (2·r2+2) + … +(2·rk-1+2) + (2·rk+1))
每一项的(2·ri+k)代表了在组件Ci上的所有IO:
- R/Sp:从Ci-1到Ci的merge读入属于Ci-1中的数据
- ri·(R/Sp):从Ci-1到Ci的merge读入属于Ci中的数据
- (r+1)·(R/Sp):将merge的结果写入
对于C0没有读取前一个组件的开销,对于Ck也没有最后。因此该公式可以简化为:
H=(2R/Sp)(Σ(ri)+k-1/2),(1≤i≤k)
化简后得:
H=(2R/Sp)·(k·(1+r)-1/2)
由此我们得到了两个重要的公式:
公式1:S = S0 + r.S0 + r2.S0 + . . . + rk.S0
公式2:H = (2R/Sp)·(k·(1+r)-1/2)
根据公式1可得:r会伴随着S0的减小而增大;根据公式2可得:H与r成正比。
得:H会随着S0的减小而增大
当LSM-Tree为两组件时
应用程序针对数据访问的总开销分为内存开销与磁盘开销,内存开销就是存储C0的存储开销,表达式为:
m·S0
存储开销是由访问IO开销与磁盘存储开销的最大值决定的,在这里的IO开销基于multi-page blcok访问频率H(pages/秒),则应用程序针对数据访问的总开销T:
T = m·S0 + max(d·S1, π·H)
由于考虑的是两组件的情况,所以k=1,r=S1/S0,令:
s = m·S0/d·S1 = 内存开销与S1数据的存储开销之比为s
t = 2·((R/Sp)/S1)·(π/d)·(m/d)
C = T/(d·S1) = 总开销与S1数据的存储开销之比
将公式2替换后得到:
C = s + max[1, t(d/m)(r + 1/2)
又r = S1/S0
得:
C = s + max[1, t(d/m)(S1/S0 + 1/2)
假设S1/S0得比值会很大,则可以将1/2消除求近似值:
C ≈ s + max[1, t(d/m)(S1/S0)
化简得:
C ≈ s + max[1, t/s]
由于磁盘访问得开销是数据访问的IO开销与存储开销的最大值,因此这也意味着:
t/s ≈ π·H / d·S1
这样,相对于开销C,就是变量t和s的函数。变量t和s的定义如下:
- t:t实际上是应用程序所需的multi-page block IO频度的某种形式化表示。对于t来说,π/d体现的是磁盘IO与空间开销之比,m/d体现的是内存开销与磁盘开销之比,这两个值是两个常量。而((R/Sp)/S1)则体现的是数据的访问密度(单位:页/bytes),如果R越大,则t越大。
- s:s代表了为实现LSM-tree我们所需要提供的内存大小。
为确定S0的大小,最简单地规则就是,沿着s=t这个分界线,此时C = s+1。同时磁盘存储和IO能力都已被完全利用。(当s=t时,由于t/s ≈ π·H / d·S1,说明此时π·H = d·S1,表示磁盘存储空间所具有的IO能力被完全使用)。
当t≤1时,在s=t时可以取得最小值;对于t>1,C的最小值是沿着曲线s=t1/2的,此时C=2·t1/2,带入等式可得:
公式3:Tmin = 2[(m·S1) · (2·π·R/Sp)]1/2
由上可得,在t≥1的情况下,LSM-tree的总开销是足以将所有LSM数据保存下来的所需内存的开销(m·S1)和用于支持将插入数据写入到磁盘所需的multi-page block IO的磁盘开销(2·π·R/Sp)的几何平均数的2倍。
总开销中的一半将会被用于S0的内存开销,剩下的一半用于对于S1的IO访问开销。
这里没有体现磁盘存储开销,因为当t≥1的情况下,IO访问的开销已经大于或等于磁盘存储开销,使的磁盘访问开销的主导是IO而不是容量。
在t≤1(数据较冷)的情况下,最小成本出现在s=t,可知C=t+1≤2。这意味在这种情况下总开销总是不会超过用于将S1存储在磁盘上的开销的两倍。在这种情况下,我们根据磁盘的存储要求来调整磁盘大小,然后使用其所有IO容量来最小化内存使用。
两组件时的例子
首先提供的数据如下:
- 插入速率R为16,000bytes/秒
- 1条索引记录为16字节
- 一个page的大小为4KB
- 考虑一个20天的周期,每天8小时
忽略其他开销,在20天之后产生的数据将是576,000,000条记录,总大小为9.2GB。对于一个两组件的LSM-Tree来说,我们需要一个大小为9.2GB的S1用于存储数据,开销就是d·S1=9600。得H=9600/π=3700 pages/秒。结合公式2,解出r=460,根据r=S1/S0,当S1为9.2GB的时候S0=20MB。此时t=0.22。
这里的计算都是估算值,并不是一个准确的值,毕竟对于计算机来说可以接受一定的误差范围内的时间开销
通过这个例子我们可以知道,在两组件LSM-tree的情况下计算C0,需要的必须参数有:
- 数据插入速率R
- 每条索引的大小
- 在C1的叶子节点中,每个page的大小
- 磁盘以multi-page blocks为单位读写一个page时的开销
- 1MB磁盘存储开销
当LSM-Tree为三组件时
当R增长10倍,意味着t也增大10倍,从0.22变为2.2,现在t就是大于1的了。利用公式2来计算出两组件LSM-tree的最小开销为$27,000,其中一半用于13.5GB的磁盘,一半用于135MB的内存。此时,仍有4.3GB的磁盘空间未被使用,加上用于缓存的2MB内存,总开销是$27,200。
插入频率R=160,000bytes/秒,意味着每秒需要有40个页面(每个页面4KB)从C0 merge到C1。因为C1大小大概是C0的68倍,因此将C0中的一个页面的merge需要读写C1中的68个页面,每秒就是5440(C0每秒40个,40·68·2=5440)个页面。这也是13.5个磁盘在使用multi-page block IO的情况下所能提供的IO能力。
对于使用一个三组件LSM-tree来处理这种R=160,000bytes/秒的情况,可以按照两组件的那种方式先计算出最大的那个磁盘组件的一个开销以及IO频率的一个开销平衡点。由于r=S1/S0,i=1,2。对于三组件来说k=2,带入公式2得:
3700+3700/r=(2·160,000/4000)·(2·(1+r)-1/2)
我们可以计算出r=23并且S0=17MB。
内存组件C0大小为17MB,稍小的那个磁盘组件大小C1是它的23倍,大概是400MB,C2又比C1大23倍,是9.2GB。那么每个页面在从C0 merge到C1时,将会引入23个页面读和23个页面写操作,这样每秒就需要读写1840(40232)个页面。类似的,每秒也需要有40个页面从C1 merge到C2,每个页面也会引入23个页面读和23个页面写操作,这样每秒也会需要读写1840(40232)个页面。这样总的IO频率就是3680,刚好是9.2G的磁盘在使用multi-page block IO的情况下所能提供的IO能力。