游戏世界中的数学工具

游戏是在计算机上实时模拟虚拟世界的数学模型。

虽然在游戏中会用到几乎所有的数学分支，但最常用的只有两种：三维矢量与矩阵。

点和矢量

物体在三维世界中的三个要素：

1. 位置（position）
2. 定向（orientation）
3. 比例（scale）

通过连续地修改这三个属性来实现动画效果，将物体变换（transform）至屏幕空间使得物体渲染到屏幕上。在游戏中三维物体几乎都是以三角形组成，三角形的三个顶点（vertex）用点（point）来表示。

坐标系

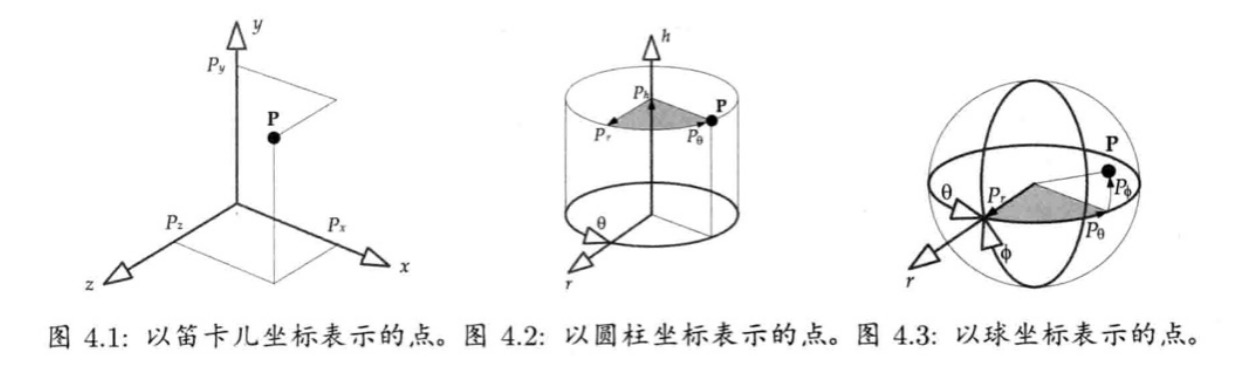
常用的坐标系有三种：

1. 笛卡尔坐标：由x、y、z三根轴组成
2. 圆柱坐标：垂直高度h，从垂直轴发射的辐射轴r，偏航角（yaw）角度θ组成
3. 球坐标：俯视角（pitch）、偏航角（yaw）、半径长度组成

坐标系选用的例子：
Q:若要让物体向漩涡一样绕着主角旋转时用什么坐标系？
A:圆柱坐标。要绘制漩涡动画，只需要简单地在θ上加上恒定角速率，在辐射轴r上加入少许向内的恒定线性速率，在h上加上向上的恒定线性速率，物体就会慢慢地旋转向上到角色中

矢量

矢量由三个标量（x、y、z）组成，即若要在三维空间中表示一个点，至少需要3个参数。

矢量v = [x, y, z]

笛卡尔基矢量

笛卡尔积单位矢量：在笛卡尔坐标系中，沿着三根轴并且模为1的矢量成为笛卡尔积单位矢量，分别表现为:

1. i = [1, 0, 0]
2. j = [0, 1, 0]
3. k = [0, 0, 1]

在笛卡尔坐标系中的任意点或矢量都能用3个标量与三个基矢量乘积之和表示标量。例如[5 3 -2] = 5i + 3j - 2k。

矢量运算

矢量与标量乘法 - 矢量的缩放

矢量a与标量s相乘，等于a中的每个分量和s相乘: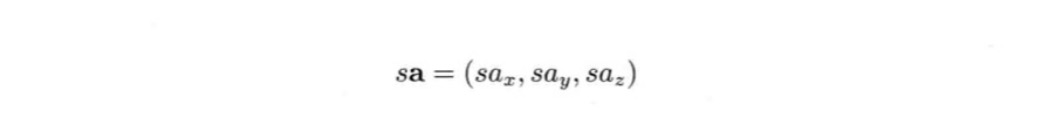

矢量与标量相乘表示矢量方向不变，缩放矢量的模，乘以-1表示将矢量方向反转（头尾互换）。其中，s被称为缩放因子(scale factor)，其中，矢量的每个轴的缩放因子也会不同，因此将矢量缩放时每个轴的缩放因子是否相同，将其分为：统一缩放和非统一缩放。非统一缩放可以表示为矢量与缩放矢量的分量积,设矢量a、缩放矢量s,则a的分量积公式如下：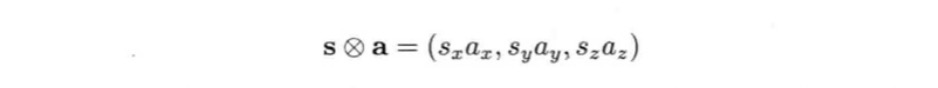

• 统一缩放：表现为标量s乘以矢量a。
• 非统一缩放：表现为两个矢量的分量积，分量积不等于两个矢量相乘。这种运算方式又被称为阿达马积。

矢量的加法与减法

矢量的相加等于将两个矢量首尾相连后剩下首尾相连所形成的新的矢量。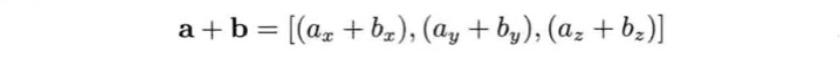

矢量的相减等同于矢量加上另一个矢量的反方向矢量。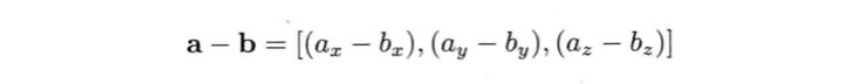

二者表现如下：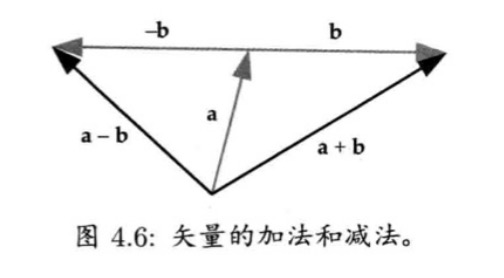

矢量与点的加减运算如下：

• 方向 + 方向 = 方向
• 方向 - 方向 = 方向
• 点 + 方向 = 点
• 点 - 点 = 方向
• 点 + 点 = 无意义

模

矢量的模等于矢量的各个标量的平方和开根号。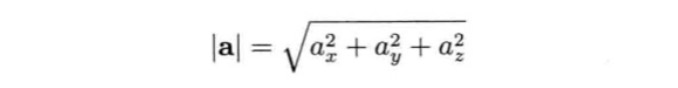

类似于勾股定理，在二维空间中，z轴为0，则可以更加直观的看到矢量模的计算：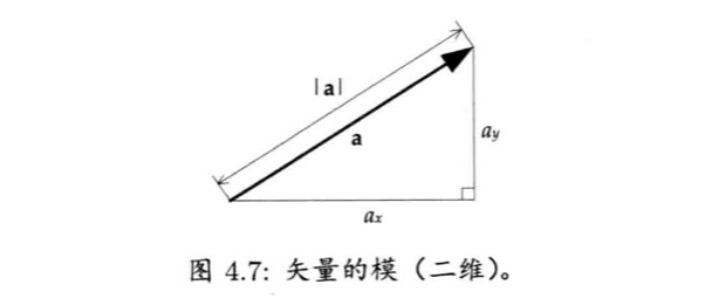

我们在进行模的比较的时候通常可以用模的平方来比较，这样可以减少开销

矢量运算的实际应用

设某人工智能的角色所在位置为P1，其速度为v，则可以找到他的下一帧位置P2，方法是把v以△t缩放，再加上P1。等式为P2 = P1 + v△t。这称为显式欧拉法。其中速度v恒定才有效。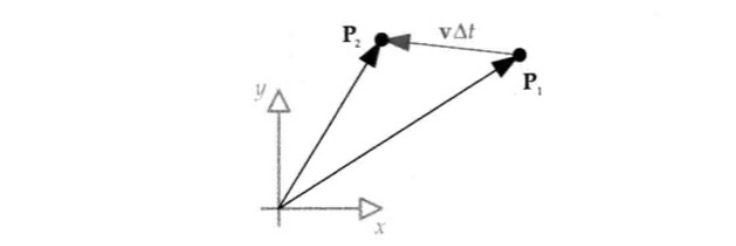

归一化与单位矢量

单位矢量：模为1的矢量

给定一个矢量v，其模为v=|v|,将其转化为方向相同的单位矢量u的过程如下：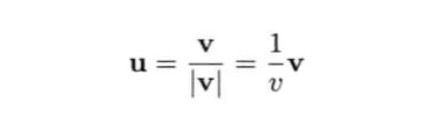

这个过程称之为归一化

法矢量

在三维世界中，一个平面可以由平面上的一点P以及一个垂直于该平面的矢量组成。这个矢量又被称为法矢量。

法矢量不等于单位矢量，他的模不一定为1

点积和投影

矢量之间可以相乘，这种相乘跟上面所描述的分量积完全不同。通常最常用的乘法有两种：

• 点积：又被称为标量积或内积
• 叉积：又被称为矢量积或外积

两个矢量的点积的结果是一个标量，这个标量等于两个矢量的各个标量相乘的和：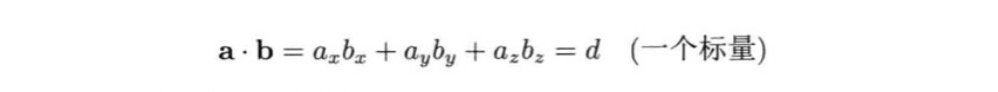

点积也可以写成两个矢量的模相乘后再乘以两个矢量之间夹角的余弦：

点积符合交换律，且在加法上符合分配律。

若u是单位矢量，则矢量a与矢量u的点积等于在u所在的直线上矢量a的投影。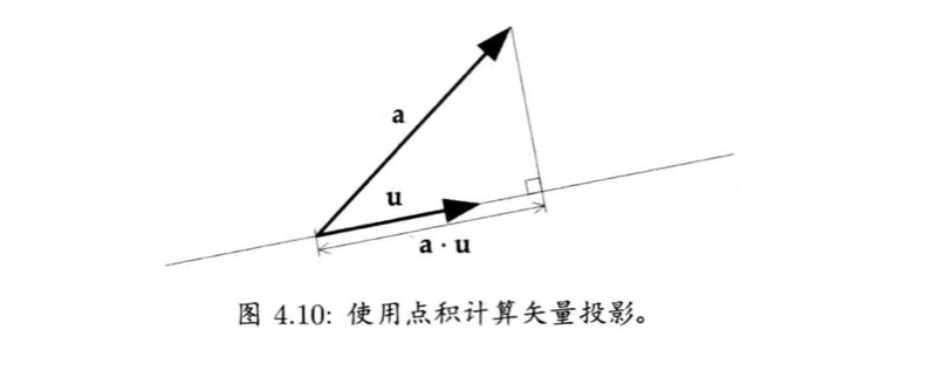

若矢量与自身相乘，由于矢量的夹角θ为0°，所谓cosθ=1，得矢量与自身的点积为矢量模的平方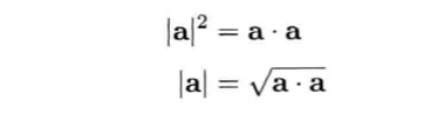

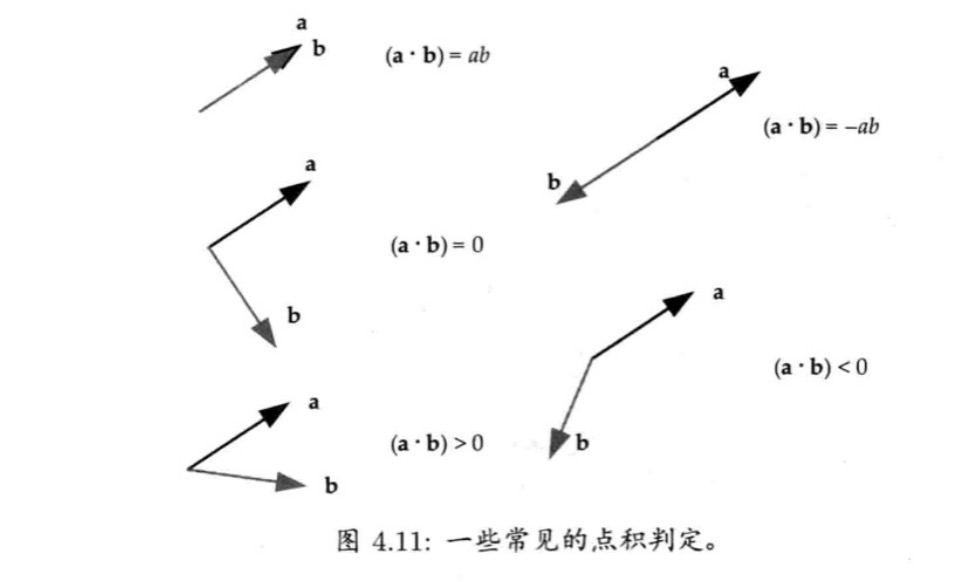
点积通常用于判断两个矢量是否共线或垂直，也可用来判断两个矢量是否大致在相同或相反方向：

• 共线：a·b=|a||b|=ab。夹角θ为0，cosθ=1
• 共线但是方向相反：a·b=-ab。夹角θ为180，cosθ=-1
• 垂直：a·b=0，cosθ=0
• 相同方向：a·b > 0(即cosθ > 0,夹角小于90°)
• 相反方向：a·b < 0(即cosθ < 0,夹角大于90°)

叉积

两个矢量的叉积会产生一个新的矢量，新的矢量垂直于相乘的两个矢量所组成的平面，因此，叉积只存在与三维空间。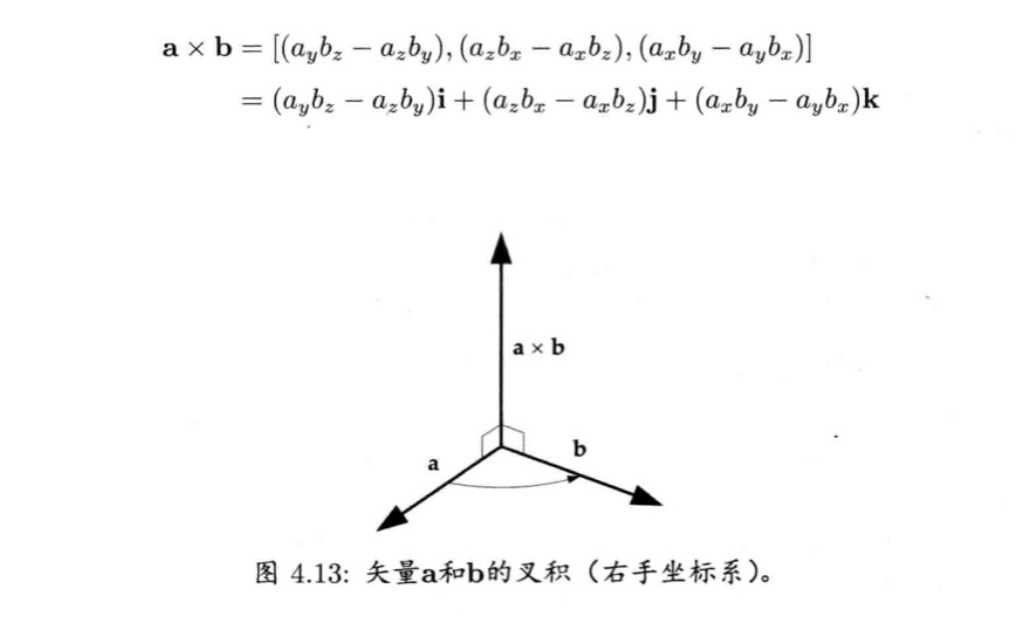

叉积的模等于两个相乘矢量的模乘以两个矢量夹角的正弦。所以当两个矢量共线时，他们的叉积为0。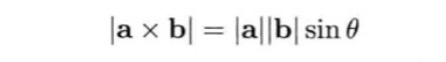

若两条矢量分别是平行四边形的两条边，则两个矢量的叉积等于这个平行四边形的面积。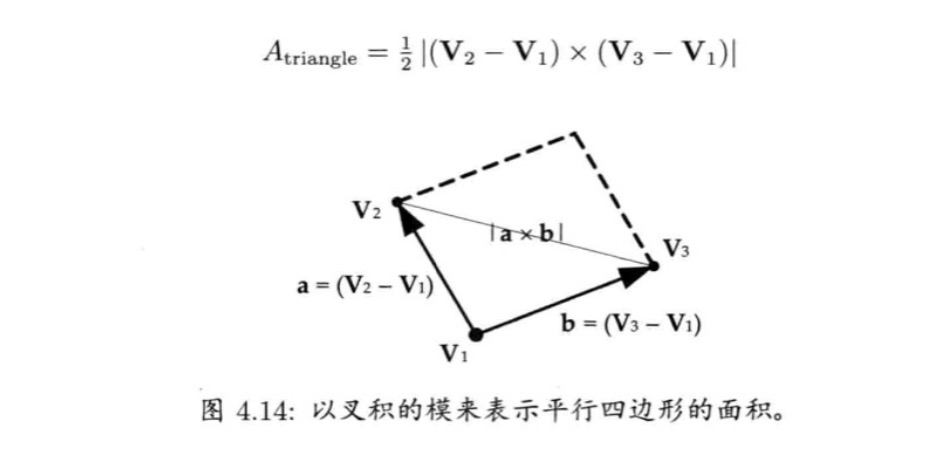

叉积的方向根据所选择的坐标系法则有关，左右法则和右手法则会得到不同方向的叉积。

叉积不符合交换律，叉积的先后顺序影响最终结果。但是符合反交换律。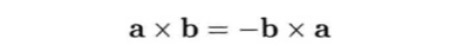

在加法上符合分配律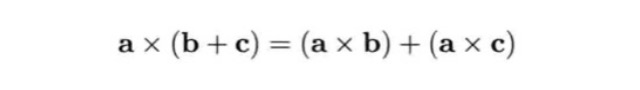

根据叉积的性质，可以得到笛卡尔积之间互相转换的公式：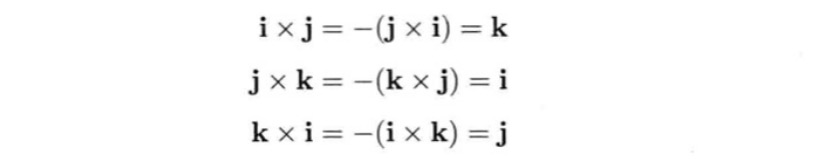

点和矢量的线性插值

在游戏中，为了保证两个点之间移动时的顺滑，需要得到点到点之间的的中间点。为了得到这个中间点的计算称为线性插值，通常简写成LERP。其定义如下，设从点A到点B，其中的中间点L与A的距离是A到B的距离的β（0 ≤ β ≤ 1）。则：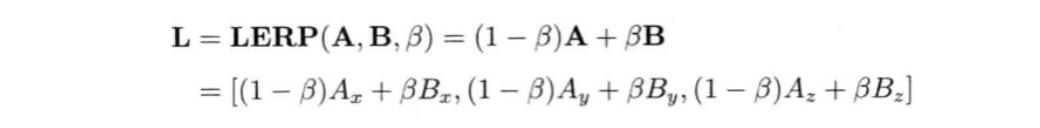

从几何上看效果如下：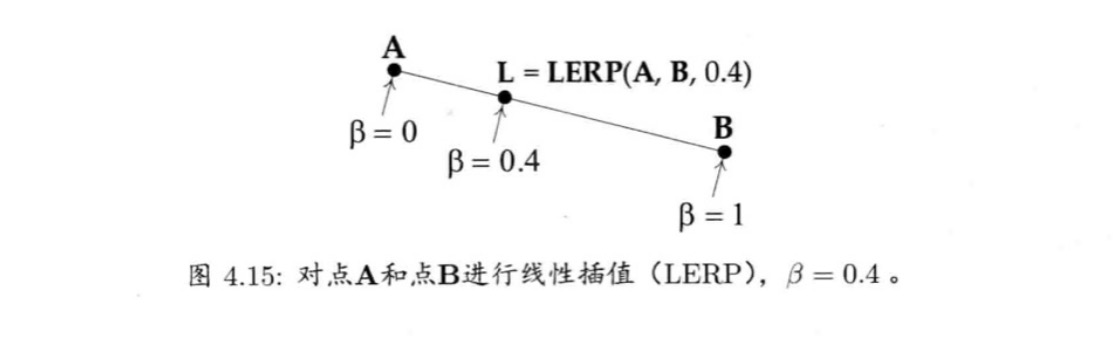

矩阵

矩阵（matrix）由mxn个标量组成的长方形数组，在游戏世界中方便用于表示旋转（transformaction）、平移（translation）、缩放（scale）。

3x3的矩阵表示纯旋转；4x4的矩阵表示旋转、平移、缩放。

矩阵乘法

当两个矩阵的内维相等的时候才能相乘，设A为m × p的矩阵，B为p × n的矩阵，那么称m × n的矩阵C为矩阵A与B的乘积，记作C=A·B。
新的矩阵的各个标量计算如下：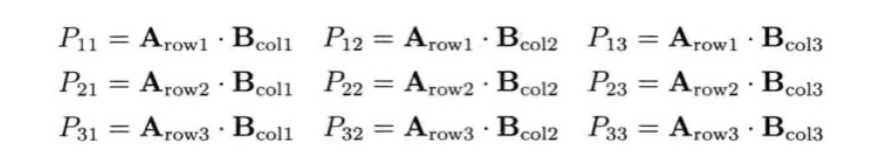

矩阵的乘法先后顺序影响最终结果，不符合乘法交换律。矩阵的乘法有时又被称为串接。因为矩阵表示一次变换，矩阵的相乘表示将多个变换串接起来。

矩阵表示点和矢量

点和矢量都可以表示为行矩阵（1 × n）或列矩阵（n × 1）。其中n表示使用中的空间纬度，通常是2或3.例如矢量v=(3 4 -1)可以写成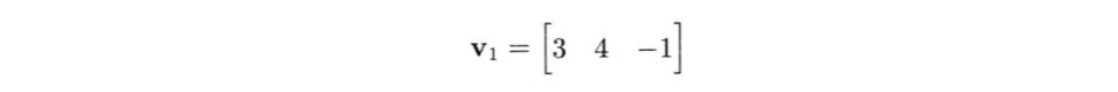

或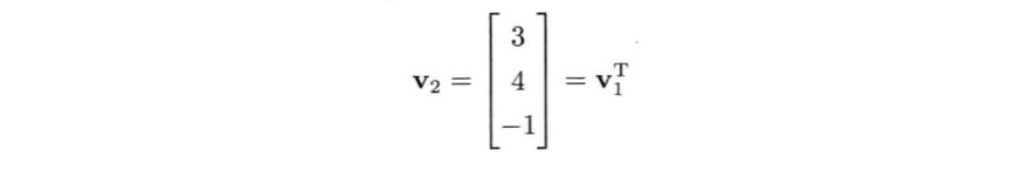

两种矩阵方式的选择会影响矩阵相乘的次序。因为矩阵相乘的时候，两个矩阵的内维需要相等。所以：

• 要把1 × n行矢量乘以n × n矩阵，矢量必须置于矩阵的左方
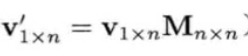
• 要把n × n矩阵乘以n × 1列矩阵，矢量必须位于矩阵的右方

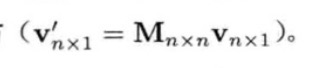
单位矩阵

单位矩阵与其他任何矩阵M相乘都等于M本身。其表现为对角线元素都是1，其他元素都是0。通常写作I。

逆矩阵

设一个矩阵为A，则它的逆矩阵表示为A⁻¹,逆矩阵能还原矩阵的变换。所以矩阵与其逆矩阵相乘结果是单位矩阵。通常用高斯消去法或LU分解求得。矩阵串街后求逆等于反向串接各个矩阵的逆矩阵。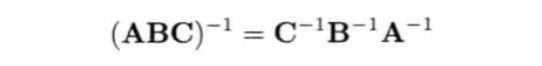

转置矩阵

矩阵M的转置写作Mᵀ,转置矩阵就是以原来矩阵的对称轴做反射。和逆矩阵一样，矩阵串接后的转置矩阵等于反向串街各个矩阵的转置矩阵。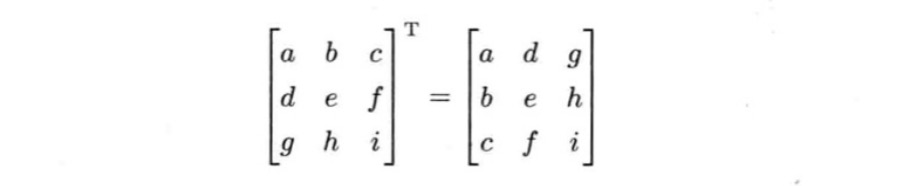

转置矩阵有一个重要的特点：

纯旋转的矩阵他的逆矩阵与转置矩阵是相同的

因此基于此，通常用转置矩阵代替逆矩阵，因为求转置矩阵的速度比求逆矩阵快。

齐次坐标

当点或矢量从三维(3 × 3)延伸至四维(4 × 4)的过程称为齐次坐标。因为4 × 4矩阵能够同时表示旋转、平移、缩放，因此在游戏中最常用的就是4 × 4矩阵。

三维空间中，若一个矢量r绕z轴旋转ø°，则可以表示为：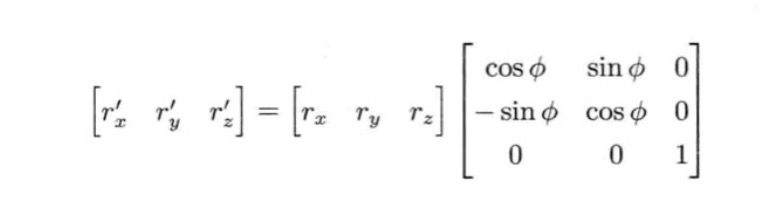

但是3 × 3矩阵无法表示平移与缩放，而4 × 4可以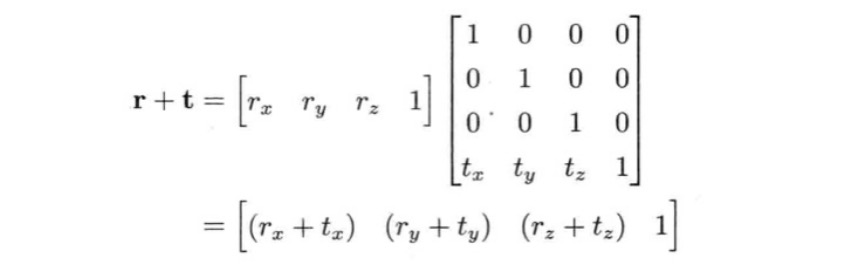

变换方向矢量

矩阵同时携带旋转、平移、缩放这三个变换信息，当矩阵作用在点上时，三者都可以产生作用。但是当用矩阵变换一个方向矢量时要忽略平移效果。因为方向矢量并不会产生平移，而且一旦平移就会改变他的模，这不是我们想要看到的。

在方向矢量与矩阵相乘是，把矢量的齐次坐标中的ω设置成0即可。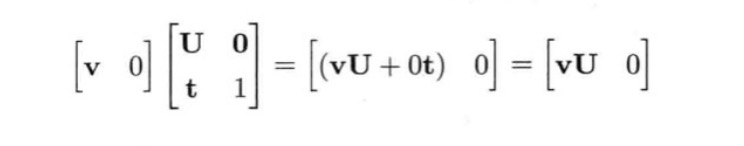

在将四维的齐次坐标转化为三维的非齐次坐标的时候通常是将x、y、z分别除以ω，因此当ω为0的时候会产生无穷大，因为在三维空间中的纯方向矢量在四维空间中表示一个无限远的点。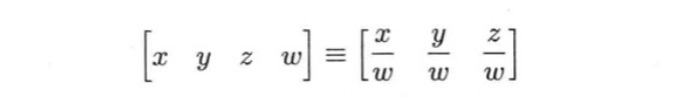

基础变换矩阵

从上可以知道4 × 4矩阵可以表示旋转、平移与缩放。他们的分布如下：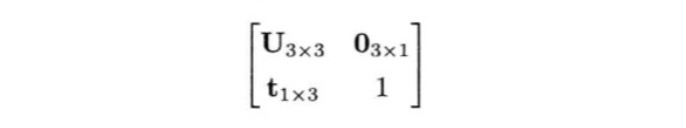

• 左上角的3 × 3矩阵U代表旋转或缩放
• 1 × 3平移矢量t
• 3 × 1矢量O = [0 0 0]ᵀ
• 右下角标量1

从中可以看到，最右边一列的标量都是常量，并不会随着矩阵的功能而改变，因此为了节省空间，在计算机中可以用4 × 3矩阵代替。

坐标空间

确定物体的具体坐标之前需要确定参照物用于构建坐标系，在三维游戏世界，根据参照物的不同将其分为三个坐标空间：世界空间、模型空间、观察空间。三者的区别如下：

• 世界空间：以游戏世界中的某点为原点，游戏世界中所有物体都可以通过世界空间表示，这个坐标将所有物体联系起来组成虚拟世界。是一个固定坐标。
• 模型空间：基于游戏中对象的坐标空间，由游戏中对象的某点为原点与其自身质点所构成的坐标系，通常是笛卡尔坐标系。
• 观察空间：又称摄像机空间，是固定在摄像机的坐标系，他的原点置于摄像机的焦点。

基的变更

上面描述的三者空间可以互相转化，即模型空间与观察空间可以转化为世界空间。这样当玩家角色与物体接触的时候通过基于同一个坐标系的数据进行判断是否产生碰撞。三个坐标构成层次关系，其中世界坐标是最底层的父坐标。

把点或者矢量从坐标系C转移到坐标系P写作Mᴄ→ᴘ,设点在坐标系C中的点坐标为Pᴄ,在坐标系P中的坐标是Pᴘ。则他们的转化公式如下：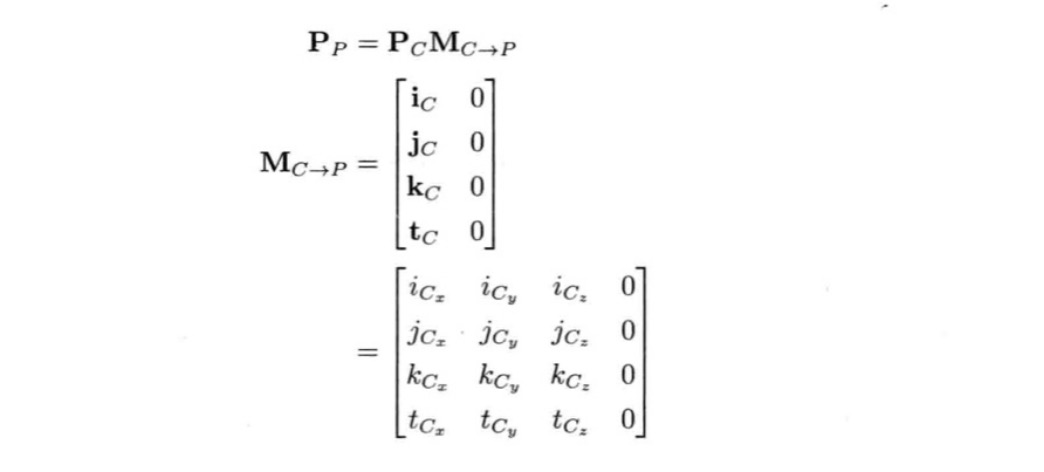

其中：

• iᴄ为子空间x轴的单位基矢量，这个矢量用父空间坐标表示
• jᴄ为子空间y轴的单位基矢量，这个矢量用父空间坐标表示
• kᴄ为子空间z轴的单位基矢量，这个矢量用父空间坐标表示
• tᴄ为子坐标系相对于父坐标系的平移

例子如下：
假设子空间绕z轴旋转角度ᵞ，没有平移，得到公式如下：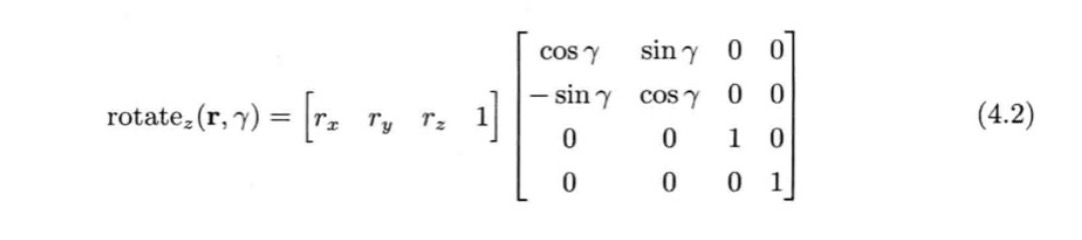

旋转示例如下：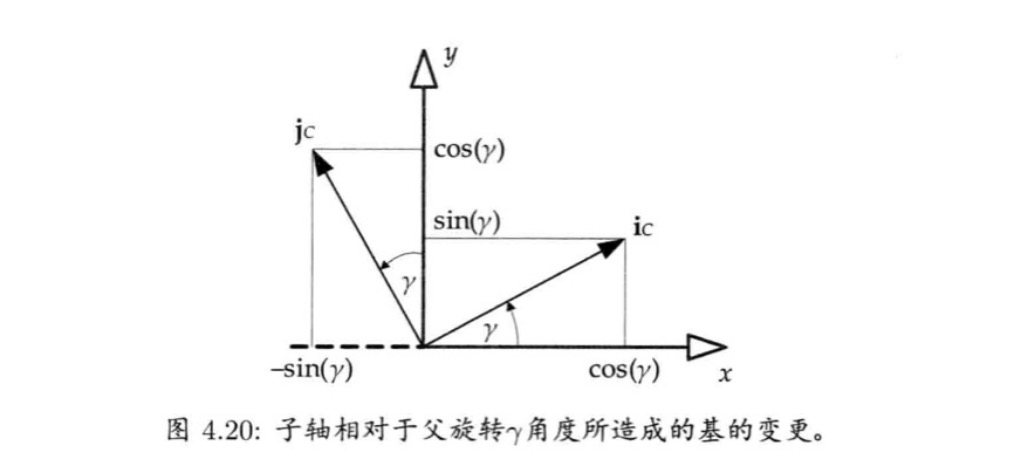

在坐标空间的变换过程中有两种选择：变换坐标系或者变换矢量：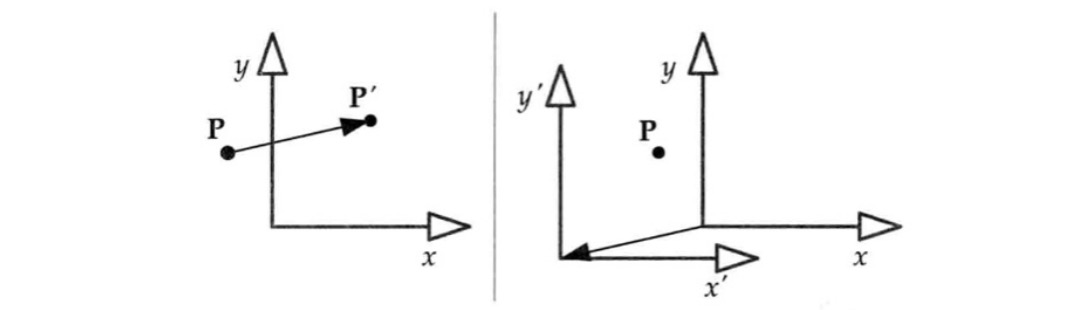

具体选择哪一种要看情况而定。

四元数

3 × 3矩阵并不是最理想的旋转表达形式，原因如下：

1. 3 × 3矩阵有9个浮点数来旋转矢量，但实际上旋转只有三个自由度（偏航角、俯仰角、滚动角）
2. 用矢量矩阵乘法来旋转矢量需要3个点积运算。
3. 在计算机图形学中，表示两个矢量位置的变换通常需要顺滑的过度，因此需要计算两个位置中间的值，这用矩阵计算很麻烦。即不能完全实现游戏对象的变换。

因此采用四元数来表示旋转，定义如下：

单位长度的四元数能代表三维旋转

即四元数中四个标量的平方和等于1的情况下都能表示三维旋转。

单位四元数视为三维旋转

四元数中有四个标量。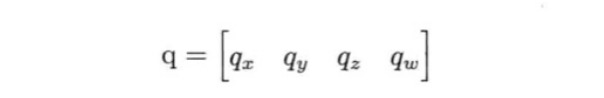

前三个标量组成的矢量v是旋转的单位轴乘以旋转半角的正弦。第四个标量qs是旋转半角的余弦。可以写成: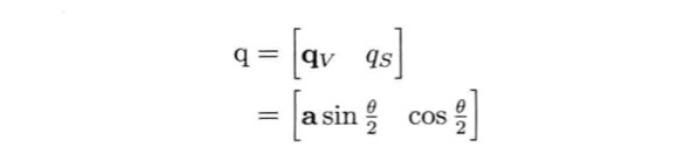

其中a为旋转轴方向的单位矢量，θ是旋转角度。旋转的方向遵守右手守则。从上面可以得到以下等式：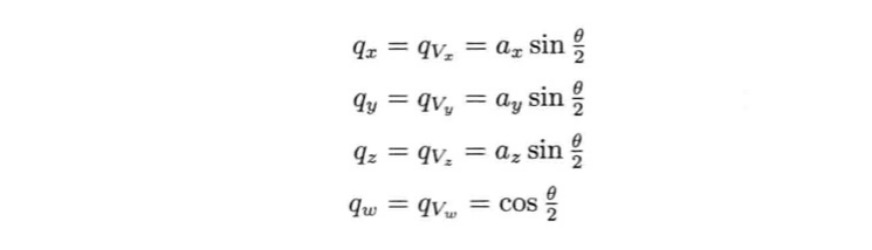

四元数运算

乘法

乘法是四元数最常用的计算方法之一，给定两个四元数q和p，他们分别代表旋转Q和P，则qp代表两个旋转的合成旋转，即先旋转Q再旋转P。这种跟旋转相关的四元数乘法又叫做格拉斯曼积，定义的pq乘积如下：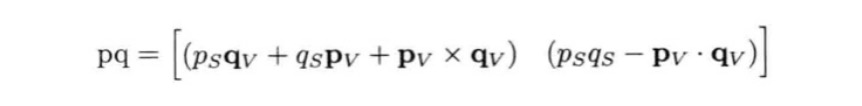

结果分成矢量部分和标量部分，其中矢量部分的结果为四元数的x、y、z，标量部分是四元数的w。

共轭以及逆四元数

四元素q的逆四元数写作q⁻¹,逆四元数和原四元数的乘积等于1.即qq⁻¹=（0i + 0j + 0k + 1）= 1.所以四元数[0 0 0 1]代表零旋转。

四元数q的共轭写作qº（这里的º应该是*，我打不出来。）定义如下：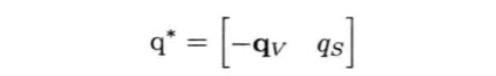

从公式中可以知道共轭是四元数矢量部分求反，但保持标量部分不变，有了这个定义，逆四元数又可以写成：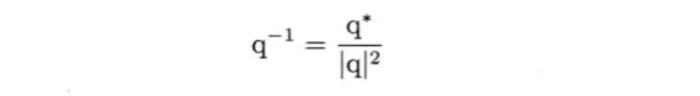

由于我们用于旋转的四元数都是单位长度，因此分母为1，化简如下：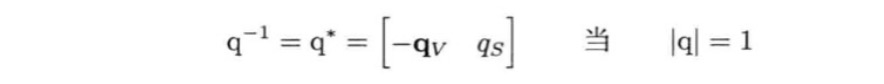

所以四元数的逆四元数等于四元数的共轭，但是求共轭的速度快于求逆。因此通常可以用共轭代替求逆的步骤。同时这也比计算3 × 3的逆矩阵快，所以这一步可以用作性能的优化。

多个四元数之积的逆四元数等于相反的逆四元数相乘，共轭同理。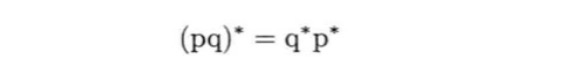

用四元数旋转矢量

用四元数旋转矢量，首先要把矢量转化为四元数形式。由于四元数比矢量多了一个标量，只要将第四个标量设置为0即可。给定矢量v,他的四元数形式表示为vᶥ=[v 0]=[x y z 0]。

要用四元数q旋转矢量v，需要先用q乘以v然后再乘以q的逆四元数。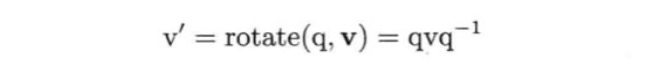

因为旋转的四元数都是单位四元数，所以可以用四元数的共轭代替逆四元数：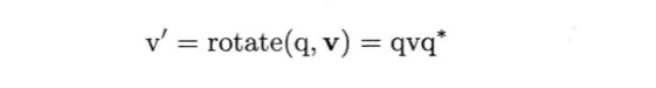

在游戏中，各个模型空间相对于世界空间就可以用四元数表示，当要将模型空间内的坐标转化为世界空间的坐标时，只需要将其乘以模型空间定量的四元数即可

四元数的串接

从上面的四元数用于矢量可以知道，四元数的串接类似于一层一层包裹矢量：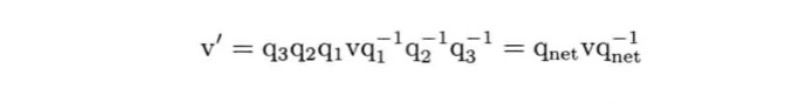

等价的四元数和矩阵

任何三维旋转都可以从3 × 3矩阵表达方式和四元数表达方式之间自由变换。设q=[qv qs] = [x y z w]，则转化为矩阵表达R如下：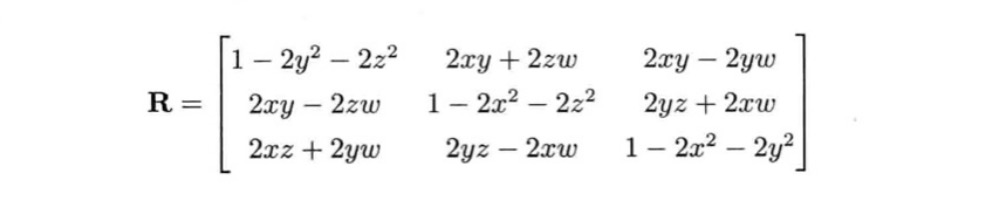

类似的，R也可以通过特定的计算得到四元数。下面是一段C/C++代码用于将矩阵转化为四元数:

#include "math.h"
#include "iostream"

void rotMatrixToQuternion(const float R[3][3], float q[4])
{
    float trace = R[0][0] + R[1][1] + R[2][2];
    
    //检测主轴
    if (trace > 0.0f) {
        float s = sqrt(trace + 1.0f);
        q[3] = s * 0.5f;

        float t = 0.5f / s;
        q[0] = (R[2][1] - R[1][2]) * t;
        q[1] = (R[0][2] - R[2][0]) * t;
        q[2] = (R[1][0] - R[0][1]) * t;
    } else {
        //主轴为负
        int i = 0;
        if (R[1][1] > R[0][0]) i = 1;
        if (R[2][2] > R[i][i]) i = 2;

        static const int next[3] = {1, 2, 0};
        int j = next[i];
        int k = next[j];

        float s = sqrt((R[i][i] - (R[j][j] + R[k][k])) + 1.0f);
        q[i] = s * 0.5f;

        float t;
        if (s != 0.0f)  t = 0.5f / s;
        else            t = s;

        q[3] = (R[k][j] - R[j][k]) * t;
        q[j] = (R[j][i] + R[i][j]) * t;
        q[k] = (R[k][i] + R[i][k]) * t;
    }
}

旋转性的线性插值

在两个旋转中间，为了保证物体变换表现的顺滑，需要获取到物体在变换时处于两个旋转中间的位置，这个点就叫做插值。

虽然两个旋转矩阵之间也可以做插值，但是他们的计算开销远远大于四元数。

最简单快捷的插值方法就是套用四维矢量的线性插值（LERP）至四元数。给定两个代表旋转A、B的四元数qᴀ、qʙ，可以找出旋转A到旋转B之间β百分点的中间旋转qʟᴇʀᴘ:

插值后的四元数需要再次归一，因为插值计算无法保证矢量长度。

在图像中体现如下：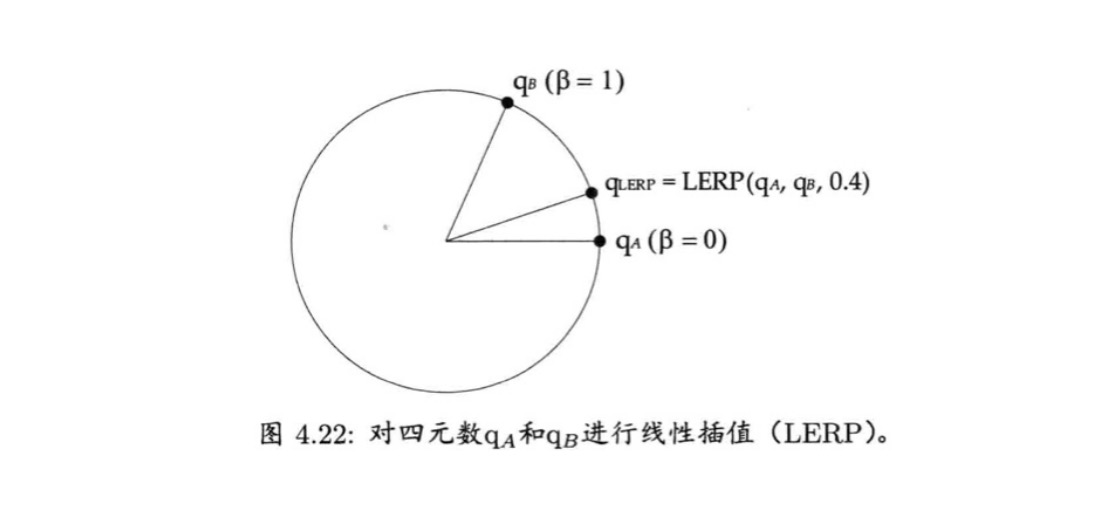

球体中的插值

LERP计算的缺点在于没有考虑四元数其实是四维超球上的点。LERP其实是沿着球体的弦进行插值，这样会导致：当β以恒定速率改变时，旋转动画并不是以恒定速率变换的，旋转会在两端慢，在中间骤然加快。为了解决这个问题产生了一个新的插值：球面线性插值（SLERP）。SLERP使用正弦和余弦在四维超球面的大圆上进行插值，而不是沿着弦上插值，这样，当β以恒定速率改变时，插值结果会以常速角速度变化。两者的区别如下：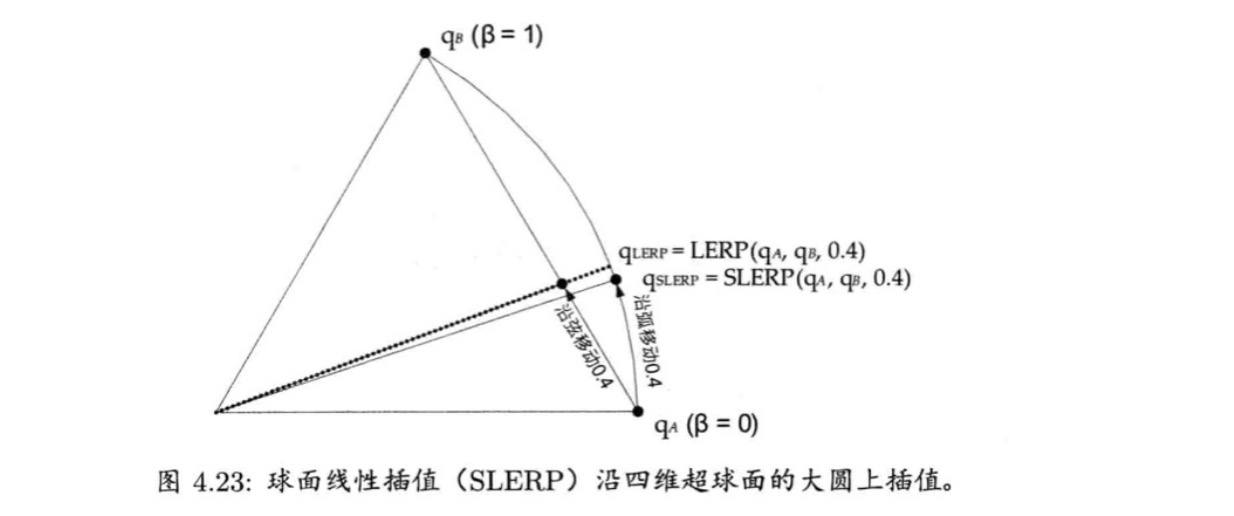

SLERP公式如下：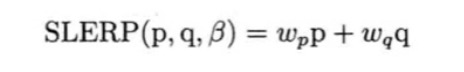

其中wᴘ和wǫ取代（1-β）和β，这两个参数使用到了两个四元数之间的正弦与余弦夹角。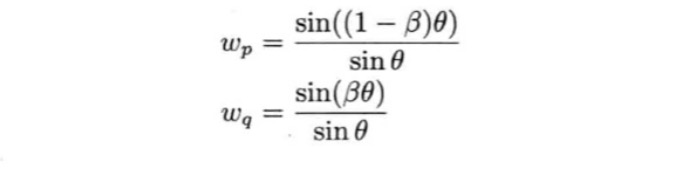

虽然SLERP比LERP更加完善，但同时计算插值的开销也更大，具体使用那种插值计算需要根据实际情况来看，在游戏中，优化也占很重要的一部分。

各种旋转

欧拉角

欧拉角能表示旋转，由三个标量组成（偏航角、俯视角、滚动角）。

优点：

• 小巧，只由3个浮点数组成
• 直观，容易把三个数值视觉化
• 对围绕单轴的旋转容易插值

缺点：

• 对任意方向的旋转不方便插值
• 会遭遇万向节死锁
• 旋转次序影响最终结果
• 依赖数据多，需要有x/y/z轴和前/左右/上方向上的映射

3 x 3矩阵

优点：

• 不受万向节锁的影响，独一无二地表达任意旋转
• 旋转可以通过矩阵乘法直接施加在矢量或点上
• 市面上大多数CPU或GPU都针对矩阵乘法做了内建支持
• 纯旋转的逆矩阵为转置矩阵，求解方便

缺点：

• 不直观，看见一个大数字表无法直观的将其想象在三维空间的变换
• 不容易插值，计算繁琐
• 占用空间大，需要占用9个存储空间

轴角

通过一个单位矢量定义旋转轴，一个标量定义旋转角表示旋转。类似于四元数表示法[旋转轴 旋转角]，写成[a θ]的形式。其中a是旋转轴、θ是旋转角。

优点：

• 表现直观，直接存在旋转轴与旋转角
• 紧凑，只占用4个存储空间

缺点：

• 无法进行简单的插值
• 轴角形式无法直接施加于点或矢量，需要将其先转化为四元数

四元数

与轴角的区别：旋转轴矢量长度为旋转半角的正弦，第四个分量是旋转半角的余弦。

优点：

• 四元数乘法能串接旋转，并把旋转直接施加于矢量和点
• 可以轻易地用LERP和SLERP进行旋转插值
• 存储空间小，只需要4个浮点数的存储空间

SQT变换

4 x 4表示任意变换（旋转、平移、缩放），但是占用空间大，因此，将四元数加上平移矢量与缩放因子来实现任意仿射变换。他的体积比4 x 4矩阵小。统一缩放只需要8个存储空间，非统一缩放需要10个存储空间。

因为统一缩放的时候缩放因子是一个标量，而非统一缩放的时候缩放因子是由三个标量组成的矢量

优点：

• 可以表示任意仿射变换
• 空间比4 x 4矩阵小
• 容易插值，各个部分可以采用不同的插值算法，平移矢量可以用LERP、四元数则可以矢量LERP或SLERP。

其他

其他还有对偶四元数、旋转和自由度等方式。