咸鱼回响

望之天回,即之云昏

0%

【剑指 offer】14- II. 剪绳子 II

发表于 更新于

来源：力扣（LeetCode）

链接：https://leetcode-cn.com/problems/jian-sheng-zi-ii-lcof

题目描述

给你一根长度为 n 的绳子，请把绳子剪成整数长度的 m 段（m、n都是整数，n>1并且m>1），每段绳子的长度记为 k[0],k[1]…k[m - 1] 。请问 k[0]k[1]…*k[m - 1] 可能的最大乘积是多少？例如，当绳子的长度是8时，我们把它剪成长度分别为2、3、3的三段，此时得到的最大乘积是18。

答案需要取模 1e9+7（1000000007），如计算初始结果为：1000000008，请返回 1。

示例 1：

1
2
3
输入: 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1

示例 2:

1
2
3
输入: 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36

提示：2 <= n <= 1000

我的解题

思路

这题根昨天的题目几乎一样，不过要注意的一点就是由于多了一个取模的条件，所以直接通过dp的max比较已经不行了。但是思路还是一样的。根据数学公式得出，数字n按照拆分的优先级分别是3、2、1，因此我们可以通过循环一个一个减去对应的数字然后保留计算结果，要注意的是，当结果已经小于等于4的时候需要特殊对待。

  • n = 4：直接结果与4相乘并退出循环呢
  • n < 3：结果与n相乘并退出循环

结果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    public int cuttingRope(int n) {
        if (n <= 3) {
            return n - 1;
        } else if (n == 4) {
            return n;
        }

        int p = 1000000007;
        long ans = 1L;
        int a = 3;
        while (n > 0) {
            ans *= a;
            ans %= p;
            n -= 3;
            if (n == 4 || n < 3) {
                a = n;
            }
        }
        return (int) ans;
    }
}

最优解

思路

数学的推导过程与上一题一样，但是在最后需要考虑大数求余的问题。针对这个问题主要有两种解决思路：

  1. 循环求余
  2. 快速冥求余

两种方法都是根据以下求余循环法则推导而成：

(xy)%p = (x%p)(y%p)%p

1.循环求余

根据上述公式推导得：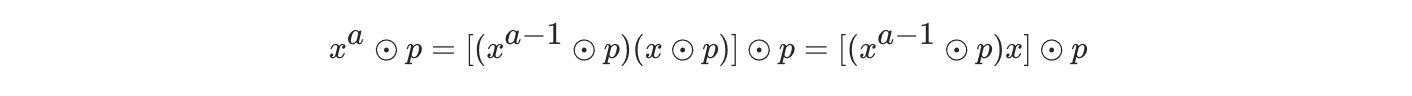



我们可以通过寻汗操作n1、n2…na对p的余数，保证每轮的中间值都在int32的范围内。

1
2
3
4
5
6
# 求 (x^a) % p —— 循环求余法
def remainder(x, a, p):
    rem = 1
    for _ in range(a):
        rem = (rem * x) % p
    return rem
2.快速冥求余

根据求余公式推导出：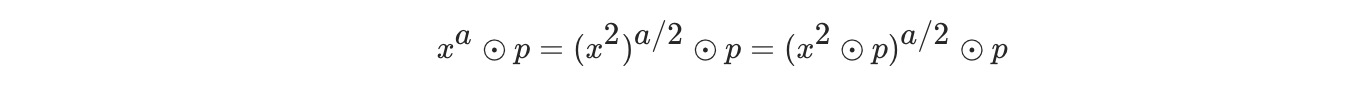



当a为奇数时，a/2不是整数，因此将其分为两种情况（“//”表示向下取整的除法）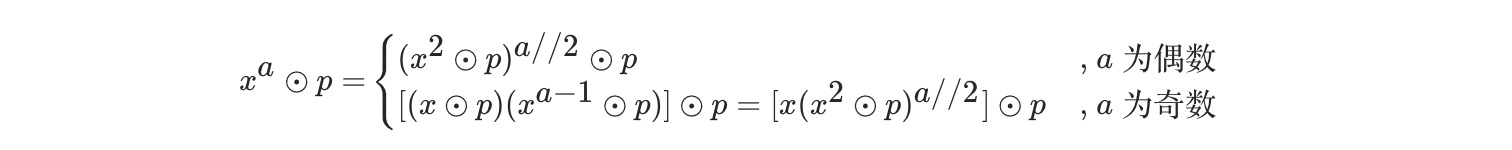


利用以上公式，可通过循环操作每次把指数 aa 问题降低至指数 a//2 问题，只需循环 log_2(N) 次，因此可将复杂度降低至对数级别。封装方法代码如下所示。

1
2
3
4
5
6
7
8
# 求 (x^a) % p —— 快速幂求余
def remainder(x, a, p):
    rem = 1
    while a > 0:
        if a % 2: rem = (rem * x) % p
        x = x ** 2 % p
        a //= 2
    return rem

结果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
    public int cuttingRope(int n) {
        if(n <= 3) return n - 1;
        int b = n % 3, p = 1000000007;
        long rem = 1, x = 3;
        for(int a = n / 3 - 1; a > 0; a /= 2) {
            if(a % 2 == 1) rem = (rem * x) % p;
            x = (x * x) % p;
        }
        if(b == 0) return (int)(rem * 3 % p);
        if(b == 1) return (int)(rem * 4 % p);
        return (int)(rem * 6 % p);
    }
}