【剑指 offer】14- I. 剪绳子

来源：力扣（LeetCode）

链接：https://leetcode-cn.com/problems/jian-sheng-zi-lcof

题目描述

给你一根长度为 n 的绳子，请把绳子剪成整数长度的 m 段（m、n都是整数，n>1并且m>1），每段绳子的长度记为 k[0],k[1]…k[m-1] 。请问 k[0]*k[1]*…*k[m-1] 可能的最大乘积是多少？例如，当绳子的长度是8时，我们把它剪成长度分别为2、3、3的三段，此时得到的最大乘积是18。

示例 1：

1
2
3

输入: 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1

示例 2:

1
2
3

输入: 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36

提示：

2 <= n <= 58

我的解题

思路

第一眼就认为用动态规划求解：设将n长的绳子分成m份后每份的乘积为f(n, m)，且 1 < m <= n,但这样就很难得到状态转移方程，因此思路不通。

后来用f(n)表示将n份绳子分成至少2份后各个结果最大的积。则f(0) = 0, f(1) = 1;后面我自己想状态转移方程就想不到了。所以还是直接看的答案。

最优解

思路

动态规划

对于的正整数 n，当 n≥2 时，可以拆分成至少两个正整数的和。令 k 是拆分出的第一个正整数，则剩下的部分是 n−k，n−k 可以不继续拆分，或者继续拆分成至少两个正整数的和。由于每个正整数对应的最大乘积取决于比它小的正整数对应的最大乘积，因此可以使用动态规划求解。

dp数组的含义： dp[i] 表示将正整数 i 拆分成至少两个正整数的和之后，这些正整数的最大乘积。
边界条件： 0 不是正整数，1 是最小的正整数，0 和 1 都不能拆分，因此 dp[0]=dp[1]=0。
状态转移方程：当 i≥2 时，假设对正整数 i 拆分出的第一个正整数是 j（1≤j<i），则有以下两种方案：
- 将 i 拆分成 j 和 i−j 的和，且 i−j 不再拆分成多个正整数，此时的乘积是 j×(i−j)；
- 将 i 拆分成 j 和 i−j 的和，且 i−j 继续拆分成多个正整数，此时的乘积是 j×dp[i−j]。

因此，当 j 固定时，有 dp[i]=max(j×(i−j),j×dp[i−j])。由于 j 的取值范围是 1 到 i−1，需要遍历所有的 j 得到 dp[i] 的最大值，因此可以得到状态转移方程如下：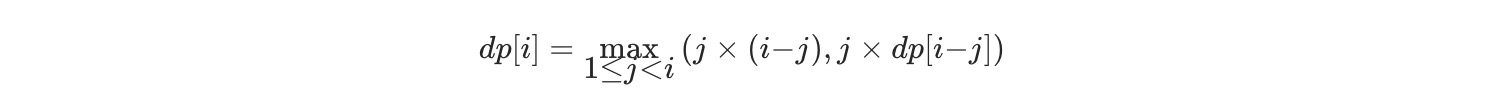

数学思想

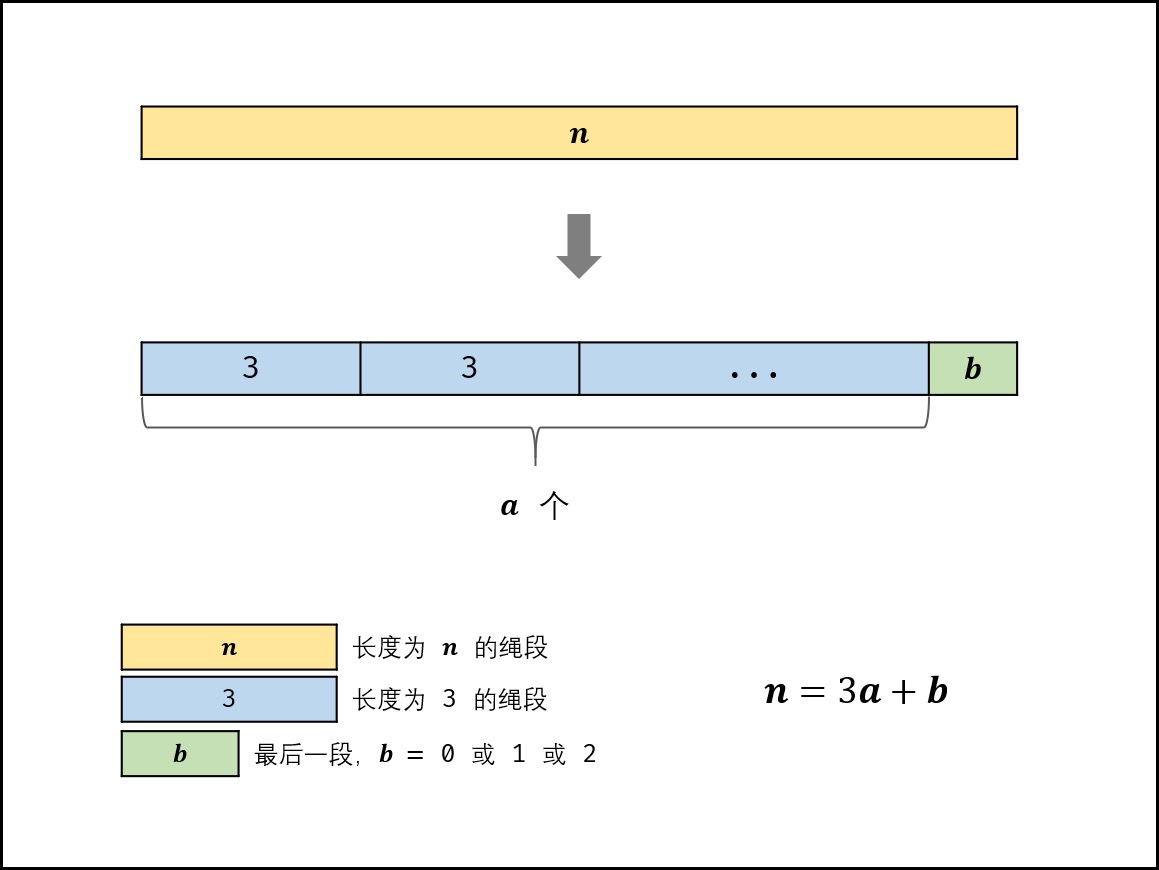
设将长度为 n 的绳子切为 a 段：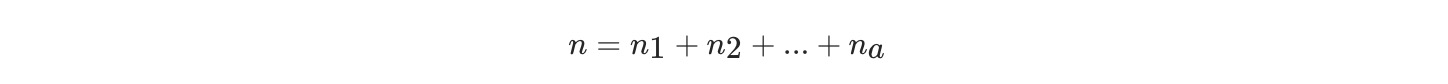

本题等价于求解：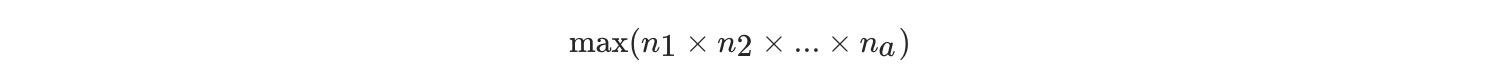

以下公式为“算术几何均值不等式” ，等号当且仅当 n1 = n2 = … = na 时候成立：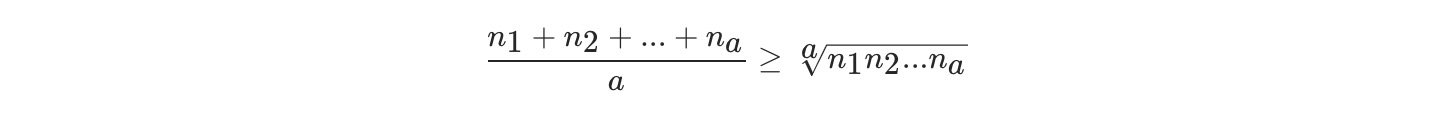

推论一：将绳子以相等的长度等分为多段，得到的乘积最大。

结果

动态规划

class Solution {
    public int cuttingRope(int n) {
        int[] dp = new int[n + 1];
        dp[0] = 0;
        dp[1] = 1;
        for (int i = 2; i <= n; i++) {
            for (int j = 1; j < i; j++) {
                dp[i] = Math.max(dp[i], Math.max(j * (i - j), j * dp[i - j]));
            }
        }
        return dp[n];
    }
}

数学思想

class Solution {
    public int cuttingRope(int n) {
        if (n <= 3) {
            return n - 1;
        }
        int a = n / 3;
        int b = n % 3;
        if (b == 0) {
            return (int) Math.pow(3, a);
        }
        if (b == 1) {
            return (int) Math.pow(3, a - 1) * 4;
        }
        return (int) Math.pow(3, a) * 2;
    }
}